散りばめられた点の中に見つかる「かたち」は？

簡単そうで難しい「離散幾何学」の問題

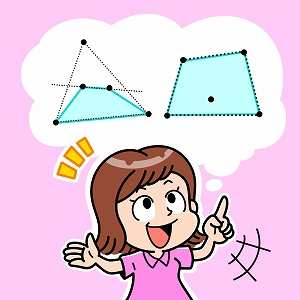
平面上に5個の点を勝手に配置します。ただし、どの3点も同一直線上にないようにします。すると、5点の中には、くぼみのない四角形（凸四角形）の頂点となる4点が必ずあります。エスター・クラインがこのことに気づいたのは、1932年頃のことです。同様に、点をどのように配置しても、凸六角形の頂点となる6点が存在するのは、何個の点があるときでしょうか？　コンピュータを使ってこの問題が解決したのは、70年以上後の2006年でした。
このような、平面上の点集合のもつ幾何学的（図形的）な組み合わせ構造は、離散幾何学の代表的な研究テーマです。一見簡単そうでありながら、実は難しい未解決問題も多く、離散幾何学の研究者の多くが関心を寄せています。

幾何学問題のコンピュータ処理を効率化

離散幾何学は20世紀後半になって急速に発展してきました。理由の一つは、日常生活に関わる幾何学的な問題をコンピュータで解決するのに、離散幾何学が役立つことです。組み合わせ的な幾何学の問題には、コンピュータで力まかせに解くのに何万年、何億年とかかってしまうものがあります。
それらを実用的な時間で解けるようにするには、計算量が少なくてすむ問題に置き換える必要があります。その際に離散幾何学の研究成果が役立ちます。離散幾何学の発展の背景には、こうしたニーズもあります。

数学が完成していく臨場感

数学は世の中の真実を解き明かす学問ですから、どのように応用できるのか、すぐにはわからない研究でも、私たちの生活に役立つときが訪れます。数学の研究は、結果そのものだけでなく、それを導く過程で生まれた副産物や解決に用いられた手法が、新たな研究分野を切り拓いたり、実生活などに応用されたりします。成長著しい離散幾何学は、今まさにその真っただ中にいます。ついこの前まで未解決問題として専門書に載っていた問題が解決されたり、既存の定理が数ヶ月ごとに次々に改良されたり、数学が完成していく臨場感をリアルタイムで味わえる研究分野です。

※夢ナビ講義は各講師の見解にもとづく講義内容としてご理解ください。

※夢ナビ講義の内容に関するお問い合わせには対応しておりません。

先生情報 / 大学情報

東海大学理学部情報数理学科教授酒井利訓先生

興味が湧いてきたら、この学問がオススメ！

離散幾何学、幾何学、離散数学、数学

先生が目指すSDGs

メッセージ

あなた自身は意識していないかもしれませんが、あなたは今、感性がとても豊かな時期です。だからこそ、自分が今まで興味や関心のなかった世界にあえて触れてみてください。例えば、絵画に興味がなかった人は展覧会に行ってみるなど、ちょっとしたことで構いません。理解しようと思わなくても構いません。あなたが今の年齢でそれらに接すること自体に意味があるのです。人に勧められたり、ポスターなどが目に入ったり、きっかけはたくさんあると思います。「やってみようかな」と思ったことがあれば、ぜひ実行してみてください。

先生への質問

先輩たちはどんな仕事に携わっているの？

東海大学に関心を持ったあなたは

海底から、宇宙まで。東海大学の学びは広がり、つながり、そして大きなうねりとなります。さまざまな場所で波を起こし、新しい波同士がぶつかり新たなひらめきが見つかることも。
東海大学は、全国のキャンパス（品川、湘南、伊勢原、静岡、熊本、阿蘇、札幌）に23学部62学科・専攻を擁する総合大学です。この大きな“受け皿”こそが、東海大学の魅力の一つです。社会に役立つ学びが集約された東海大学なら、あなたの興味や情熱に応える学びがきっと見つかります。