数学者には見える、「ドラクエ」のような世界

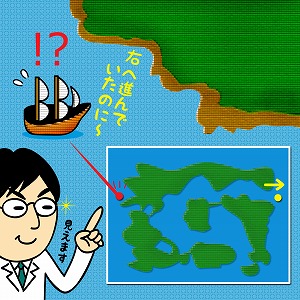
ドラクエの世界は球体ではない

一般の人はすべての物体を「x、y、z」の座標で示せる、いわゆる3次元ユークリッド空間として認識しています。しかし数学者は空間をもっと自由な、グニャグニャ曲がりくねったものとしてとらえています。そうした観点から見ると、球面は無数の小さな平面が貼り合わさったものとなります。そしてある平面上の一点は、違う平面の対応する一点と同じだとみなすのです。
例えば、ゲーム「ドラゴンクエスト」で船で右へ進んでいたのに、いつの間にか地図の左の方にいたという経験はありませんか？　ドラクエの世界は左右の端にある座標が対応関係にあり、それを貼り合わせるとドーナツのような形になります。上下にも同じことが言えますから、ドラクエは左右と上下2つのドーナツが組み合わさった世界となります。数学者はこのような形で空間を認識しているのです。

宇宙には何通りものモデルがある

そうした視点から宇宙をとらえると、実は数学的に矛盾のないモデルがたくさんあり、何通りもの可能性が考えられます。本来、物理学的には宇宙の形はひとつに決まっていた方がわかりやすいのですが、何通りもの可能性があると、「なぜ人間が存在するのはこの世界なのか？」という、新たな理由が必要になってしまいます。
矛盾を解決する理論として物理学から生まれたのが、「ミラー対称性」という考え方です。簡単に言うと、何通りもの宇宙モデルはすべて正しいのですが、人間の目ではある同じ形に見えるというものです。

異なる空間で問題を考える

相関関係にある2つの空間を結び付けて考える方法は、数学のさまざまな問題を解決するのに役立ちます。例えば、Aという空間で複雑だった問題がBという空間では簡単に解けることがあり、その解法を用いればAでの問題も解けるといったことが可能になるのです。さまざまな空間を並行して調べることで数学的な理解が深まるとわかったことで、ミラー対称性は現在、世界中で活発に研究されているのです。

※夢ナビ講義は各講師の見解にもとづく講義内容としてご理解ください。

※夢ナビ講義の内容に関するお問い合わせには対応しておりません。

先生情報 / 大学情報

東京都立大学理学部数理科学科准教授赤穂まなぶ先生

興味が湧いてきたら、この学問がオススメ！

シンプレクティック幾何学

メッセージ

数学には明確な式と答えがあるイメージですが、実際は違います。
実は、数学の世界は「おそらくこうなるのでは？」という予想であふれ、そもそも問題自体が確定していないものも多いのです。例えば、「○○＝△△」という予想の右辺は定義できていても、左辺は定義すらできていない、そういうものがたくさんあります。数学はあまりにも高度化し、もはや研究者1人の手で解き明かせるものではなくなってきています。ある意味、すべての人に解決に寄与するチャンスがあると言えるでしょう。

東京都立大学に関心を持ったあなたは

東京都立大学は「大都市における人間社会の理想像の追求」を使命とし、東京都が設置している公立の総合大学です。人文社会学部、法学部、経済経営学部、理学部、都市環境学部、システムデザイン学部、健康福祉学部の7学部23学科で広範な学問領域を網羅。学部、領域を越え自由に学ぶカリキュラムやインターンシップなどの特色あるプログラムや、各分野の高度な専門教育が、充実した環境の中で受けられます。